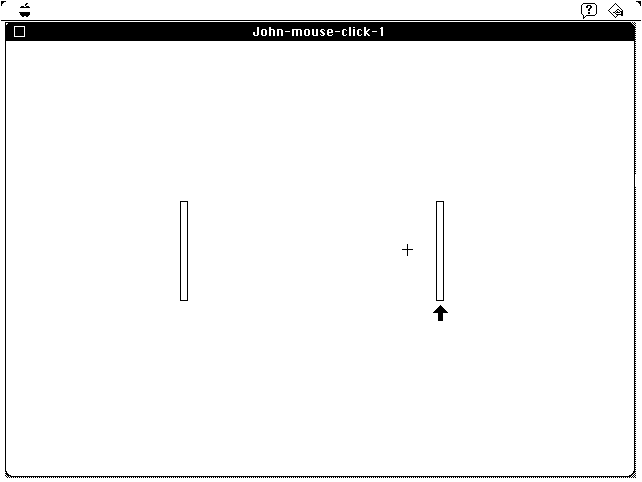
Figure 1. A typical screen showing Fitts' reciprocal tapping
task
(point-and-select) as implemented for a CRT display and any input device.
2Computer Systems Research Institute
University of Toronto
Toronto, Ontario, Canada M5S 1A4
In this paper, we will describe MODEL BUILDER, a program that builds Fitts' law prediction models for any input device that can connect to the Apple Macintosh. One objective herein is, in a simplistic sense, to "publish" MODEL BUILDER - to make the program available to anyone with electronic mail access to INTERNET. The program resides on a file server at the University of Guelph and may be retrieved using file-transfer-protocol (ftp).
There is no shortage of utility programs in the public domain; but tools specifically aimed at research are generally not offered. There are three objectives in publishing Model Builder in this way. First, it seems an appropriate (but neglected) use of technology to facilitate the ability of others to duplicate or test our results. Second, it permits others to extend our research to other devices and conditions in such a way that results are more easily compared. Third, we are interested in contributing to HCI education by making the tool available to students and instructors.
We call MODEL BUILDER a "rapid" evaluation tool since it immediately
performs a statistical analysis on performance data and provides a linear
regression prediction equation, coefficient of correlation, and a plot
of the regression line with scatter points. The number of trials upon which
the evaluation is based defaults to 160 but is user-selectable through
a setup screen. Data files are created and saved permitting in-depth, follow-up
analyses across multiple devices, trial blocks, subjects, or any other
experimental condition of interest.
One of the most robust and highly adopted models of human movement is Fitts' law (Fitts, 1954). Fitts' information processing model has been used widely in previous HCI research and holds considerable promise as a tool for design (Card, Mackinlay, & Robertson, 1990; MacKenzie, in press, 1992; Marchionini & Sibert, 1991; Newell & Card, 1985). Typical examples of the law in HCI research include Boritz, Booth, & Cowan (1991); Card, English, and Burr (1978); Gillan, Holden, Adam, Rudisill, and Magee (1990); MacKenzie, Sellen, and Buxton (1991); Walker and Smelcer (1990); and Ware and Mikaelian (1987).
The following paragraphs briefly summarize Fitts' law. For detailed reviews, see Buxton (in press), MacKenzie (1992), or Meyer, Smith, Kornblum, Abrams, and Wright (1990).
According to Fitts' law, the time (MT) to move to and select a target of width W which lies at distance (or amplitude) A is
MT = a + b log2(2A/W)
(1)
where a and b are constants determined through linear regression. W corresponds to "accuracy" -- the required region where an action terminates. The log term is the index of difficulty (ID) and carries the unit "bits" (because the base is 2). If MT is measured in "seconds", then the unit for a is "seconds" and for b, "seconds/bit". The reciprocal of b is the index of performance (IP) in "bits/second". This is the human rate of information processing for the movement task under investigation.
Variations of the law have been proposed by Welford (1968),
MT = a + b log2(A/W + 0.5), (2)and MacKenzie (1989),
MT = a + b log2(A/W + 1). (3)Equations 1, 2, and 3 differ only in the formulations for ID. On the whole, Equation 3, known as the Shannon formulation, is preferred because it
Unfortunately, substantial theoretical and methodological problems exist
in applying Fitts' law, with the result that the potential to actually
use prediction models (or metrics such as bandwidth), is seriously compromised
(MacKenzie, 1992). An example is error rate. Although a technique exists
for normalizing responses to accommodate the speed-accuracy tradeoff, it
is rarely applied. The technique, first described by Crossman in 1960 (Welford,
1968, p. 147), calls for target width (W) to be transformed into
an effective target width (We) reflecting the spatial
variability in subjects' actions. All Fitts' law models built in such a
manner carry an inherent, nominal error rate of 4%. Performance metrics
such as bandwidth are more accurate and more useful if they encompass both
the speed and accuracy of responses. Furthermore, models derived in such
a manner can be compared with confidence that the differences found are
due to inherent properties in devices, tasks, etc., rather than to experimental
procedures or hidden factors that may have induced behaviour at different
points on the speed-accuracy continuum.

Figure 1. A typical screen showing Fitts' reciprocal tapping
task
(point-and-select) as implemented for a CRT display and any input device.
The design mimics that employed by Fitts (1954) in his original experiments using a stylus. The distance between the targets (the amplitude, A) and the width of the targets (W) each vary over four levels with
A = {64, 126, 256, 512} pixels, and
W = {8, 16, 32, 64} pixels.
The easiest condition has A = 64 and W = 64 for a task difficulty
of
ID = log2(A/W + 1) = 1.00 bit.The hardest condition has A = 512 and W = 8 for a task difficulty of
ID = log2(A/W + 1) = 6.02 bits.The sixteen A-W conditions are presented in random order with a block of trials performed at each condition. The default is 10 trials per block. At the end of each block, the screen goes blank for about 1 second and then the next condition appears. A selection outside the target is considered an error and is accompanied by a beep.
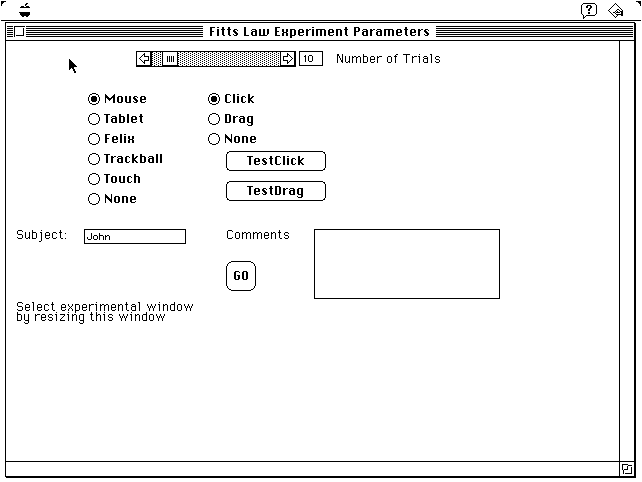
Figure 2. Set-up screen. Several parameters can be set to control
the
characteristics of the session and the format of the output file. The
GO
button initiates a block of trials.
The TESTCLICK and TESTDRAG buttons initiate a single block of warmup
trials and return immediately to the setup screen. Anything entered in
the SUBJECT or COMMENTS box is written to the output data file. The GO
button initiates the sixteen blocks of trials for model building.
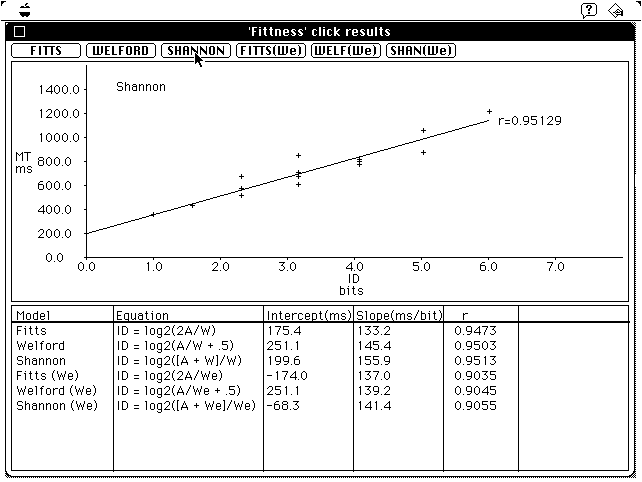
Figure 3. The results screen. A scatter plot and regression
line are
displayed using one of six possible Fitts' law models. The Shannon
model using
un-normalized values for target width (W) is displayed.
All six models are given at the bottom of the display. The coefficients shown include the intercept and slope of the regression line and the correlation. Figure 4 is the same except the normalized Shannon model has been selected for display. The prediction model for this plot is
MT = -68 + 141 log2(A/We + 1). (4)
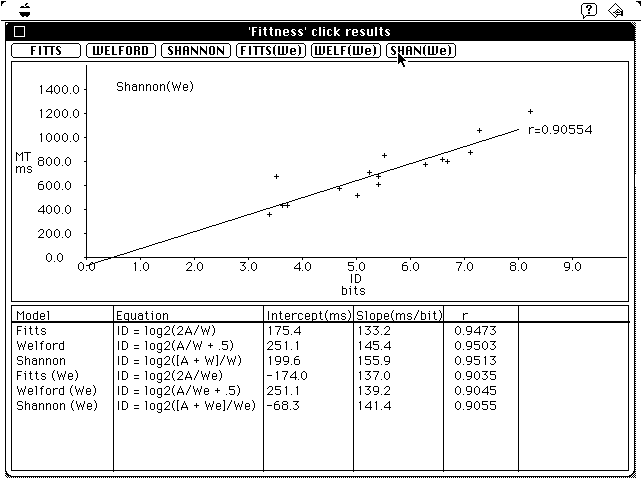
We should mention that the technique for normalizing is applied at the
model building stage only. The transformation of target width (W)
into the effective target width (We) is based on the
spatial variability in a block of trials. In applying the model to predict
the time for a single trial, it is W that is used in the prediction
equation. Using a model built with normalized measures implies that subsequent
predictions carry a 4% probability that the target will be missed (MacKenzie,
1992; Welford, 1968, p. 147).
The bandwidth associated with the prediction model in Equation 4 is the reciprocal of the slope coefficient, namely
1 / 141 = 7.1 bit/s.As shown in Figures 3 and 4 the correlations increased slightly from the Fitts to the Welford to the Shannon formulations; however, the correlations on the whole were lower using normalized measures. Since the sample is small and based on a single subject, we shall not dwell further on the differences in correlations. Note, however, that in a re-analysis of Fitts' (1954) data the correlations were slightly higher when the regression models were built using normalized data (MacKenzie, 1989, 1992).
======================================== Experiment: Fitts' Law Click Experiment Comment: Subject: John Device: mouse Task: click Session: 1 Number of Blocks: 16 Trials per block: 10 Block A= 64 W= 8 58 -4.5 -22 40 0.5 -23 43 -1.5 -24 53 2.5 -27 35 -0.5 -26 45 -1.5 -26 44 1.5 -26 62 2.5 -26 56 -0.5 -26 100 -3.5 -30 Block A= 64 W= 16 27 -0.5 -14 **** etc. **** ========================================
For each trial three measurements are recorded: the time (in clock ticks,
1/60 s), and the X and Y pixel coordinates of selection.
The first trial took (58/60) x 1000 = 967 ms. The Y coordinate is
saved but it is not used. The X coordinate is normalized about the
centre of the target. A negative value indicates the selection was on the
"inside" of target-centre, toward the centre of the screen. Since the width
of each target was an even number of pixels, no pixel corresponded to the
precise centre of the target; hence, the ".5" weighting for each X
coordinate. The occurrence of an error was not explicitly saved, but is
easily determined from the X coordinate and the target width. With
W
= 8 in the first block in Figure 5, selections were on-target if -3.5 <=
X <= +3.5, or off-target otherwise. As evident in Figure 5, one
error occurred in the first block of trials for this session.
========================================================== % ftp snowhite.cis.uoguelph.ca !connect to our archive name: anonymous password: name@site !enter your name and site ftp> cd pub/fitts-law !change directory ftp> dir !mb.Hqx should appear ftp> get mb.Hqx !retrieve model builder ftp> get README ftp> quit ==========================================================
After retrieval, Binhex or a related utility must be used to
convert MODEL BUILDER from a hex file to a binary application. Some additional
information may be found in a README file which should also be retrieved.
This research was supported by the Natural Sciences and Engineering
Research Council of Canada, Xerox Palo Alto Research Center, Digital Equipment
Corp., and Apple Computer Inc. We gratefully acknowledge this contribution,
without which, this work would not have been possible.
Buxton, W. (in press). Haptic input to computer systems. Cambridge, UK: Cambridge University Press.
Card, S. K., English, W. K., & Burr, B. J. (1978). Evaluation of mouse, rate-controlled isometric joystick, step keys, and text keys for text selection on a CRT. Ergonomics, 21, 601-613.
Card, S. K., Mackinlay, J. D., & Robertson, G. G. (1990). The design space of input devices. Proceedings of the CHI '90 Conference on Human Factors in Computing Systems (pp. 117-124). New York: ACM.
Fitts, P. M. (1954). The information capacity of the human motor system in controlling the amplitude of movement. Journal of Experimental Psychology, 47, 381-391.
Greenstein, J. S., & Arnaut, L. Y. (1988). Input devices. In M. Helander (Ed.), Handbook of human-computer interaction (pp. 495-519). Amsterdam: Elsevier.
Gillan, D. J., Holden, K., Adam, S., Rudisill, M., & Magee, L. (1990). How does Fitts' law fit pointing and dragging? Proceedings of the CHI '90 Conference on Human Factors in Computing Systems (pp. 227-234). New York: ACM.
MacKenzie, I. S. (1989). A note on the information-theoretic basis for Fitts' law. Journal of Motor Behavior, 21, 323-330.
MacKenzie, I. S. (1992). Fitts' law as a research and design tool in human-computer interaction. Human-Computer Interaction, 7, 91-139.
MacKenzie, I. S. (in press). Movement time prediction in human-computer interfaces. Proceedings of Graphics Interface `92. Toronto: Canadian Information Processing Society.
MacKenzie, I. S., Sellen, A., & Buxton, W. (1991). A comparison of input devices in elemental pointing and dragging tasks. Proceedings of the CHI '91 Conference on Human Factors in Computing Systems (pp. 161-166). New York: ACM.
Marchionini, G., & Sibert, J. (1991). An agenda for human-computer interaction: Science and engineering serving human needs. SIGCHI Bulletin, 23(4), 17-32.
Meyer, D. E., Smith, J. E. K., Kornblum, S., Abrams, R. A., & Wright, C. E. (1990). Speed-accuracy tradeoffs in aimed movements: Toward a theory of rapid voluntary action. In M. Jeannerod (Ed.), Attention and performance XIII (pp. 173-226). Hillsdale, NJ: Erlbaum.
Milner, N. P. (1988). A review of human performance and preferences with different input devices to computer systems. In D. Jones & R. Winder (Eds.), People and Computers IV: Proceedings of the Fourth Conference of the British Computer Society -- Human-Computer Interaction Group (pp. 341-362). Cambridge, UK: Cambridge University Press.
Newell, A., & Card, S. K. (1985). The prospects for psychological science in human-computer interaction. Human-Computer Interaction, 1, 209-242.
Thomas, C., & Milan, S. (1987). Which input device should be used with interactive video? In B. Shackel (Ed.), Human-Computer Interaction -- INTERACT `87 (pp. 587-592). Amsterdam: Elsevier.
Walker, N., & Smelcer, J. B. (1990). A comparison of selection times from walking and pull-down menus. Proceedings of the CHI `90 Conference on Human Factors in Computing Systems (pp. 221-225). New York: ACM.
Ware, C., & Mikaelian, H. H. (1989). A evaluation of an eye tracker as a device for computer input. Proceedings of the CHI+GI '87 Conference on Human Factors in Computing Systems and Graphics Interface (pp. 183-188). New York: ACM.
Welford, A. T. (1968). Fundamentals of skill. London: Methuen.